本篇文章给大家谈谈排列组合和公式,以及排列组合公式的知识点,希望对各位有所帮助,不要忘了收藏本站!
排列组合公式是高二年级的数学。
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。 排列组合与古典概率论关系密切。
发展历程:
虽然数学始于结绳计数的远古时代,由于那时社会的生产水平的发展尚处于低级阶段,谈不上有什么技巧。
随着人们对于数的了解和研究,在形成与数密切相关的数学分支的过程中,如数论、代数、函数论以至泛函的形成与发展,逐步地从数的多样性发现数数的多样性,产生了各种数数的技巧。
同时,人们对数有了深入的了解和研究,在形成与形密切相关的各种数学分支的过程中,如几何学、拓扑学以至范畴论的形成与发展,逐步地从形的多样性也发现了数形的多样性,产生了各种数形的技巧。
高中数学排列组合公式
排列A(n,m)=n×(n-1)。(n-m+1)=n!/(n-m)!(n为下标,m为上标,以下同)。
组合C(n,m)=P(n,m)/P(m,m)=n!/m!(n-m)!。
例如A(4,2)=4!/2!=4*3=12。
C(4,2)=4!/(2!*2!)=4*3/(2*1)=6。
加法原理与分布计数法:
1、加法原理:做一件事,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法...在第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+m3+.. +m种不同方法。
2、第一类办法的方法属于集合A1,第二类办法的方法属于集合A2...第n类办法的方法属于集合An,那么完成这件事的方法属于集合AUA2....UAn。
3、分类的要求:每一类中的每一种方法都可以独立地完成此任务;两类不同办法中的具体方法,互不相同(即分类不重) ;完成此任务的任何一种方法,都属于某一类(即分类不漏)。
高中排列组合公式是:C(n,m)=A(n,m)/m!=n!/m!(n-m)!与C(n,m)=C(n,n-m)。
例如C(4,2)=4!/(2!*2!)=4*3/(2*1)=6,C(5,2)=C(5,3)。
排列组合c计算方法:C是从几个中选取出来,不排列,只组合。
C(n,m)=n*(n-1)*...*(n-m+1)/m!
例如c53=5*4*3÷(3*2*1)=10,再如C(4,2)=(4x3)/(2x1)=6。
两个常用的排列基本计数原理及应用:
1、加法原理和分类计数法:
每一类中的每一种方法都可以独立地完成此任务,两类不同办法中的具体方法,互不相同(即分类不重),完成此任务的任何一种方法,都属于某一类(即分类不漏)。
2、乘法原理和分步计数法:
任何一步的一种方法都不能完成此任务,必须且只须连续完成这n步才能完成此任务,各步计数相互独立。只要有一步中所采取的方法不同,则对应的完成此事的方法也不同。
cn2排列组合公式:
C(n,2)
=n!/(2!x(n-2)!)
n!可以写成nx(n-1)x(n-2)!,所以上面的式子可以写成:
(nx(n-1)x(n-2))/(2x(n-2)!)
=n(n-1)/2
cn2的意思是从n个中取2个无排列的个数,排列组合是组合学最基本的概念,排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
两个常用的排列基本计数原理及应用:
1、加法原理和分类计数法:
每一类中的每一种方法都可以独立地完成此任务,两类不同办法中的具体方法,互不相同(即分类不重),完成此任务的任何一种方法,都属于某一类(即分类不漏)。
2、乘法原理和分步计数法:
任何一步的一种方法都不能完成此任务,必须且只须连续完成这n步才能完成此任务,各步计数相互独立。只要有一步中所采取的方法不同,则对应的完成此事的方法也不同。
排列的公式:A(n,m)=n×(n-1)……(n-m+1)=n!/(n-m)!(n为下标,m为上标,以下同)。组合的公式:C(n,m)=P(n,m)/P(m,m) =n!/m!×(n-m)!。
排列组合,排列在组合之前,咱们要聊的第一个概念是“排列”,排列的英文是 Permutation 或者 Arrangement,因此在数学符号中,用 P 或者 A 表示都可以,二者意思完全一样。我们常见的 P 右边会跟两个数字(或字母),右下角的数字 n 表示总数,右上角的数字 m 表示抽出的个数。
排列组合
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。 排列组合与古典概率论关系密切。
排列的定义:从n个不同元素中,任取m(m≤n,m与n均为自然数,下同)个不同的元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数。
以上内容参考: ——排列组合
关于排列组合和公式,排列组合的公式有哪些并举列说明介绍到此就结束了,不知道你从中找到你需要的信息了吗 如果你还想知道更多这方面的信息,记得收藏关注本站。
富时A50指数的成份股有哪些?1、a50成分股主要有:中...
今天阿莫来给大家分享一些关于华为真正入股的a股上市公司和华为深度合作...
长沙邮箱是多少?1、湖南交通职业技术学院联系电话073...
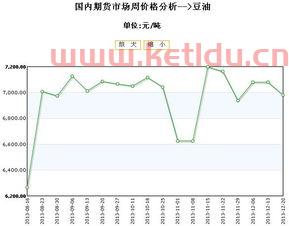
*豆油期货行情1、截至11月26日,大商所豆油主力合约...
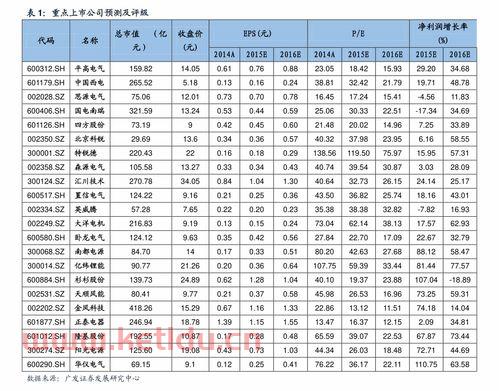
这是当然的受国际金价波动影响着*的时候达到1920美元/盎司一:...