在投资世界里,谁都想把“未来的回报”算得清清楚楚,但股票作为权益工具,收益率的计算并不是一个简单的数字游戏,而是要把风险、时间和现金流放在同一张标尺上来衡量。所谓股票要求的收益率,就是在你承受特定风险水平的前提下,投资这只股票你愿意或需要得到的最小回报。这个数字不是固定的,它会随着市场环境、公司基本面、行业周期和个人风险偏好而变化。本文以自媒体式的活泼风格,系统拆解几种主流的计算 *** ,帮助你把“我要多少回报才能买这股”这件事说清楚。
一、为什么要有一个“要求收益率”的概念,以及它在投资决策中的作用。简单说,任何投资都带来机会成本,也意味着你的资金有替代路径。你希望通过这笔资金获得比无风险资产更高的收益,同时还承担了与之相匹配的风险。要求收益率就是这个“比无风险高多少、要承担多大风险”的平衡点。它不是一个单独的估值值,而是你用来对比估值、计算是否值得买入的参照线。拿到一个清晰的要求收益率后,你就可以用不同的估值 *** 去判断股票的“合理价格区间”。
二、主流的计算框架:CAPM、股息折现模型(DDM)与成长股的变体。CAPM(资本资产定价模型)把收益率分解成无风险收益、市场风险溢价以及个股的系统性风险暴露;股息折现模型则把未来股息作为核心现金流,通过股息增长预期来贴现回现在的价格,常用于有稳定股息的公司;对成长型但不一定分红的股票,可以用成长折现法或“增长率近似法”等替代,但核心还是现金流贴现的思想。继续往下看,你会看到具体的公式、输入项和适用场景。
三、CAPM:公式、要素与操作步骤。CAPM的核心公式是:R_e = R_f + β ×(R_m − R_f)。其中,R_e 是股票的要求收益率(成本权益),R_f 是无风险利率,β 是股票相对于市场的风险暴露度,R_m 是市场的期望收益率,(R_m − R_f) 即市场风险溢价。要点在于:β 越高,股票对市场波动的敏感度越大,要求收益率越高;R_f 越低,基线越低,但在极端低利率环境下也可能拉高市场估值。实际操作中,你会先选取一个公认的无风险利率基准(如国债收益率或国债收益率曲线上的某个期限点),再用公开来源的β 值或通过回归分析得到的β 值,最后用市场预期收益率或历史市场收益率来近似 R_m。将这些输入带入公式,你得到的 R_e 就是你对这只股票的“最低可接受回报”。
四、股息折现模型(DDM):Gordon 模型与应用。对于有稳定股息政策的公司,股息折现模型提供另一条直观路径。最基本的 Gordon Growth Model 形式是:P = D1 / (R − g),其中 P 是当前股价,D1 是明年股息,R 是投资者的要求回报率(同样也可视为成本权益),g 是股息的永续增长率。换成要求回报率的表达:R = D1 / P + g。也就是说,股票的回报来自两部分:一是来自股息现金流的收益率 D1/P,二是股息增长带来的资本增值 g。实操中,D1 需要对明年的股息进行假设,P 是现在的市场价格,g 则常用历史增长率、行业增长趋势或管理层展望来估算。但要注意,DDM 对“稳定分红且增速可持续”的前提要求较强,遇到分红波动、增长不可持续时就要谨慎使用。
五、成长股的“输入要点”与替代 *** 。很多成长股并不稳定支付股息,直接使用 DDM 会很困难。此时可以采用“近似法”或“成长股贴现法”:把未来现金流与公司自由现金流(FCF)结合,按一定的贴现率贴现到现在,得到企业价值,再扣除债务得到股本价值。关键在于对未来现金流、增长率和资本结构的假设要合理、要有区间分析。另一种简化路径是通过“收益法”来估算成本权益:设定一个合理的未来收益增长假设,用市盈率、价格/销售比率等倍数来对比市场上的类似标的,从而间接得到一个对比的回报水平。无论选用哪种 *** ,核心都是把未来现金流的不确定性分解到不同场景(乐观、基线、悲观)并进行敏感性分析。
六、关键输入项的获取与校验技巧。风险无风险利率 R_f 的选取要考虑期限与货币单位,一般以长期国债收益率或无风险国债曲线上的点来近似;β 值可以从权威金融数据供应商获取,也可以用自有回归模型对历史市场数据进行估算,注意滚动更新以适应市场波动;市场风险溢价 (R_m − R_f) 的取值通常在历史区间的中位数或均值附近波动,常见区间在 4%~6%之间,实际选择要结合宏观经济情景和行业周期进行调整;D1、g、FCF、增发/回购等因素需要从公司披露、行业研究和分析师预测中综合得到,记得对未来情景进行敏感性分析,看看结果对输入的变动有多敏感。实际操作中,三种模型往往给出三种不同的“合理回报区间”,把它们放在一个合适的区间并进行交叉验证,是稳健投资的表现之一。
七、一个简单的对照示例,帮助把公式落地。设想某股票当前价格 P 为 100 元,明年的股息 D1 预期为 3 元,预计股息增长率 g 为 5%,风险无风险利率 R_f 为 2%,市场预期收益率 R_m 为 8%,β 为 1.2。用 CAPM,R_e = 2% + 1.2 × (8% − 2%) = 2% + 1.2 × 6% = 2% + 7.2% = 9.2%。用 DD M,R = D1/P + g = 3/100 + 5% = 0.03 + 0.05 = 8%。可见两种 *** 给出的结果就有差异,CAPM 给出的是一个更高的风险贴现率,DDM 则把股息与增长率直接折现到价格层面。若你仅以这两种结果做对比,可能会发现估值的敏感性来自于输入假设的不同。你可以进一步用一个“保守-基线-乐观”三点场景来看看结果的区间化表现,例如把 D1、g、β 的取值在一个合理范围内跑几遍,看看 R_e 的区间分布。
八、实际投资中的应用要点。不同 *** 的结果并不总是一致,原因在于模型假设、现金流可得性、市场情绪等因素。实务上常做的不是单一数字,而是建立一个“多模型对比+ 情景分析”的框架:1) 先给出一个你愿意接受的回报区间;2) 用 CAPM、DDM 与成长折现法得到各自的回报区间;3) 对比这些区间是否落在你设定的可接受区间内;4) 如果价格低于综合评估的底线,就可能被认为具备买入潜力,反之则保持观望。对于风险偏好较高的投资者,可以适度对高 β 股票采用更严格的估值折现;对偏保守的投资者,可以多用稳健的股息股票和更保守的增长假设进行分析。
九、常见误区与纠偏诀窍。第一,过度依赖单一模型,忽视输入假设的敏感性;第二,β、R_f、R_m 等输入值的时效性与区域性很强,跨市场应用需谨慎;第三,成长股的股息不稳定时,DDM 的适用性下降,应优先考虑基于自由现金流的贴现或其他 *** ;第四,忽视交易成本、税费、流动性等现实因素;第五,市场心态会让“理论价格”与“市场价格”出现暂时错位,错位并不总是有套利机会,要结合基本面做长期判断。
十、把理论变成决策工具的小贴士。先明确你的投资目标、风险承受能力和时间 horizon,再把 CAPM、DDM 和成长法的结果放在同一个对比表中,标出关键输入的区间和敏感性图。常用的做法是:做一个三点场景分析(乐观、基线、悲观),在每个场景下给出 R_e 的取值,以及对应的合理价格区间。这样的练习不仅能帮助你理解股票的“回报与风险”之间的关系,还能在市场波动时帮助你保持清晰的决策方向。现在你已经掌握了从无风险利率、β、市场溢价到股息、增长率的完整链条,下一步就是在你熟悉的市场里用真实数据跑一遍,看看自己的“回报门槛”是不是还稳稳地站在合理区间之内。
脑筋急转弯:如果 CAPM 给出的要求收益率总是恰好等于你对市场的预期回报,但市场却总是很难稳定地达到这个水平,你会更相信模型还是价格,还是你已经在用另一种隐形的利率在买卖?
富时A50指数的成份股有哪些?1、a50成分股主要有:中...
今天阿莫来给大家分享一些关于华为真正入股的a股上市公司和华为深度合作...
长沙邮箱是多少?1、湖南交通职业技术学院联系电话073...
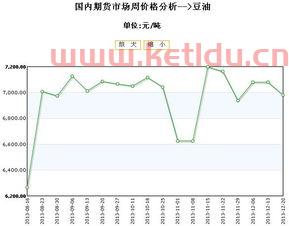
最新豆油期货行情1、截至11月26日,大商所豆油主力合约...
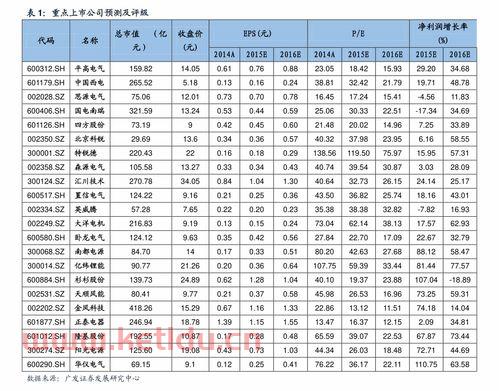
这是当然的受国际金价波动影响着最高的时候达到1920美元/盎司一:...